Computer Graphics 101

Das große Ganze

Bevor wir uns mit der Low-Level-Implementierung befassen, überlegen wir, was das Ziel ist. Wir wollen eine 3D-Szene – eine Ansammlung von Objekten und Lichtern – beschreiben und bestimmen, wie diese aus einem bestimmten Kamerawinkel aussehen würde. Im Allgemeinen gibt es zwei Möglichkeiten, dies zu erreichen. Eine besteht darin, durch jedes Pixel zu gehen und zu bestimmen, welchen Weg ein Photon hätte nehmen müssen, um darauf zu landen, und daher rückwärts zu arbeiten, um seine Farbe herauszufinden.

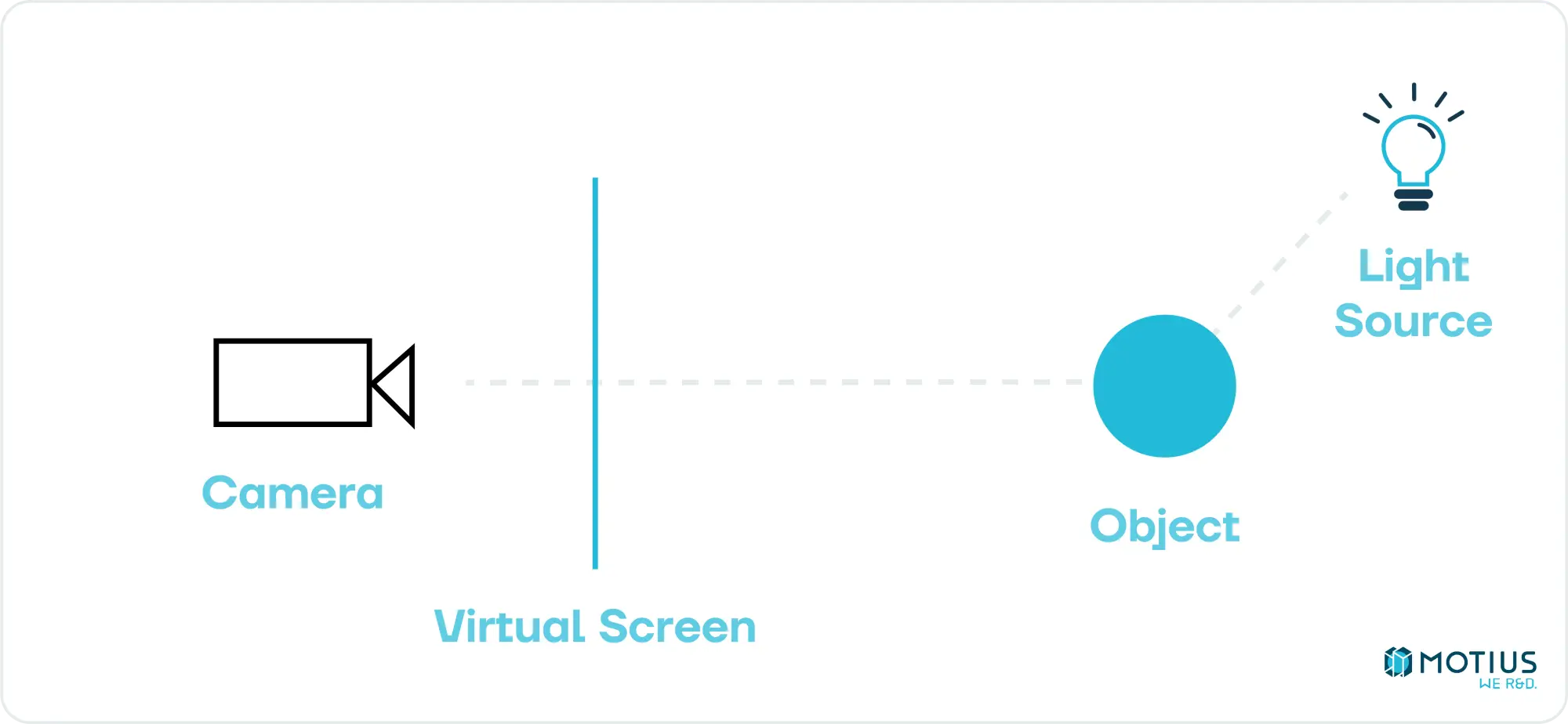
Dies wird als Raytracing bezeichnet. Obwohl es konzeptionell einfach ist, ist es sehr ressourcenintensiv (jedes Pixel muss einen Strahl werfen, der viele Male abprallen kann). Es liefert großartige Ergebnisse, ist aber in der Regel zu langsam für Echtzeitanwendungen. In letzter Zeit hat sich dies mit der zunehmenden Leistung von GPUs ein wenig verschoben und Raytracing wird unter bestimmten Umständen zusammen mit unserem anderen Ansatz verwendet. Aber dies ist eine Studie der Grundlagen, nicht des Stands der Technik.

Der andere Ansatz ist als Rasterung bekannt. Die Hauptidee besteht darin, das Objekt in einfache Teile zu zerlegen und dann zu bestimmen, wie dieser Teil der Kamera erscheinen würde. Die einfachste 3D-Oberfläche ist ein Dreieck, und daher wird es normalerweise als unser Grundelement verwendet (d.h. das, in das wir komplexe Objekte zerlegen). Jedes Dreieck im dreidimensionalen Raum kann auf eine virtuelle Leinwand projiziert werden und wird dort durch ein zweidimensionales Dreieck (oder ein Liniensegment, wenn die Ebene des Dreiecks senkrecht zu unserem Bildschirm steht) dargestellt:

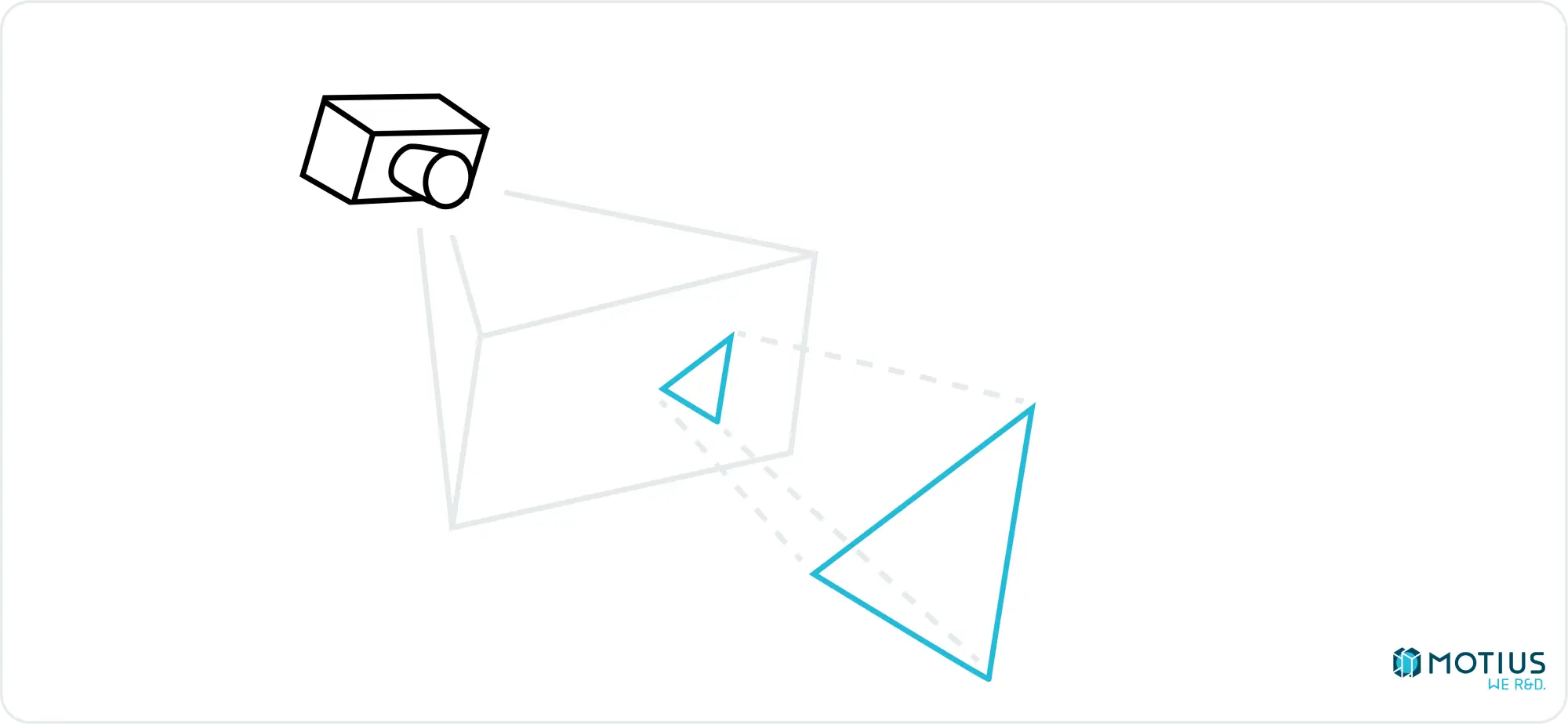
Wenn wir also wissen, wie man ein Dreieck in 2D zeichnet und wie man die 3D- → 2D-Projektionen durchführt, können wir jede 3D-Form zeichnen, oder zumindest eine Annäherung an eine. Es wird aus flachen Dreiecken bestehen. Aber es gibt einige Tricks, zu denen wir später noch kommen werden, die diese Tatsache größtenteils verbergen werden.

Zuerst werde ich mich auf das Zeichnen von 2D-Dreiecken vorbereiten, und dann werden wir 3D- → 2D-Projektionen durchführen. In späteren Teilen dieser Serie werden einige Optimierungen und Beleuchtungstechniken vorgestellt, um die Wiedergabetreue dessen, was wir zeichnen können, zu verbessern.

Zeichnen von Pixeln

Bevor wir irgendetwas anderes tun können, müssen wir in der Lage sein, ein einzelnes Pixel auf den Bildschirm zu zeichnen. Wie du das tust, hängt von deinem Setup ab. Ich werde Typescript in einem Browser verwenden und dabei eine HTML-Leinwand als Renderziel verwenden. Diese Wahl basiert ausschließlich darauf, dass es einfach ist und die Tools verwendet werden, die ich gut kenne. Wir brauchen nur einen Ort, an dem wir anfangen können, um zu interessanten Problemen zu gelangen.

 
function drawPixel(x: number, y: number, r: number, g: number, b: number) {
  const canvas = document.querySelector(im Folgenden "#canvas")
  const context = canvas.getContext('2d')
  context.fillStyle = 'rgb(${color.r}, ${color.g}, ${color.b})'
  context.fillRect(x, y, 1, 1)
}
 

Setzt Pixel (x, y) auf Farbe (r, g, b). Es gibt sicherlich effizientere Möglichkeiten, dies zu tun, aber wenn wir diesen Weg einschlagen, würden wir am Ende einfach webGL verwenden. Es erledigt die Arbeit, die wir brauchen, und wir müssen unsere Schlachten aussuchen.

Hinweis zu meinen Code-Snippets: Viele meiner Code-Snippets werden aus Gründen der Übersichtlichkeit im Kontext des Dokuments bearbeitet. In der Praxis würde ich die Leinwand und den Kontext nicht für jedes Pixel bekommen, das ich zeichnen möchte. Dies würde einmal außerhalb dieser Funktion erfolgen. Einige Snippets verwenden auch Typen, die ich vielleicht nicht explizit definiere, aber als offensichtlich betrachte (z. B. sollte Vector2 einfach genug sein. Sie fragen sich vielleicht, ob es sich um ein Array oder ein Objekt in Javascript handelt, aber das wird bald durch die Art und Weise klar, wie es verwendet wird).
Ich werde meinen vollständigen Code am Ende teilen, aber wenn du zu Hause mitmachen willst, müsstest du dein Gehirn ein wenig einsetzen, um aus meinen Schnipseln nützliche Funktionen zu machen.

Koordinate Systeme

Dies ist ein guter Punkt, um 2D-Koordinatensysteme zu besprechen. HTML-Canvas verwendet Folgendes:

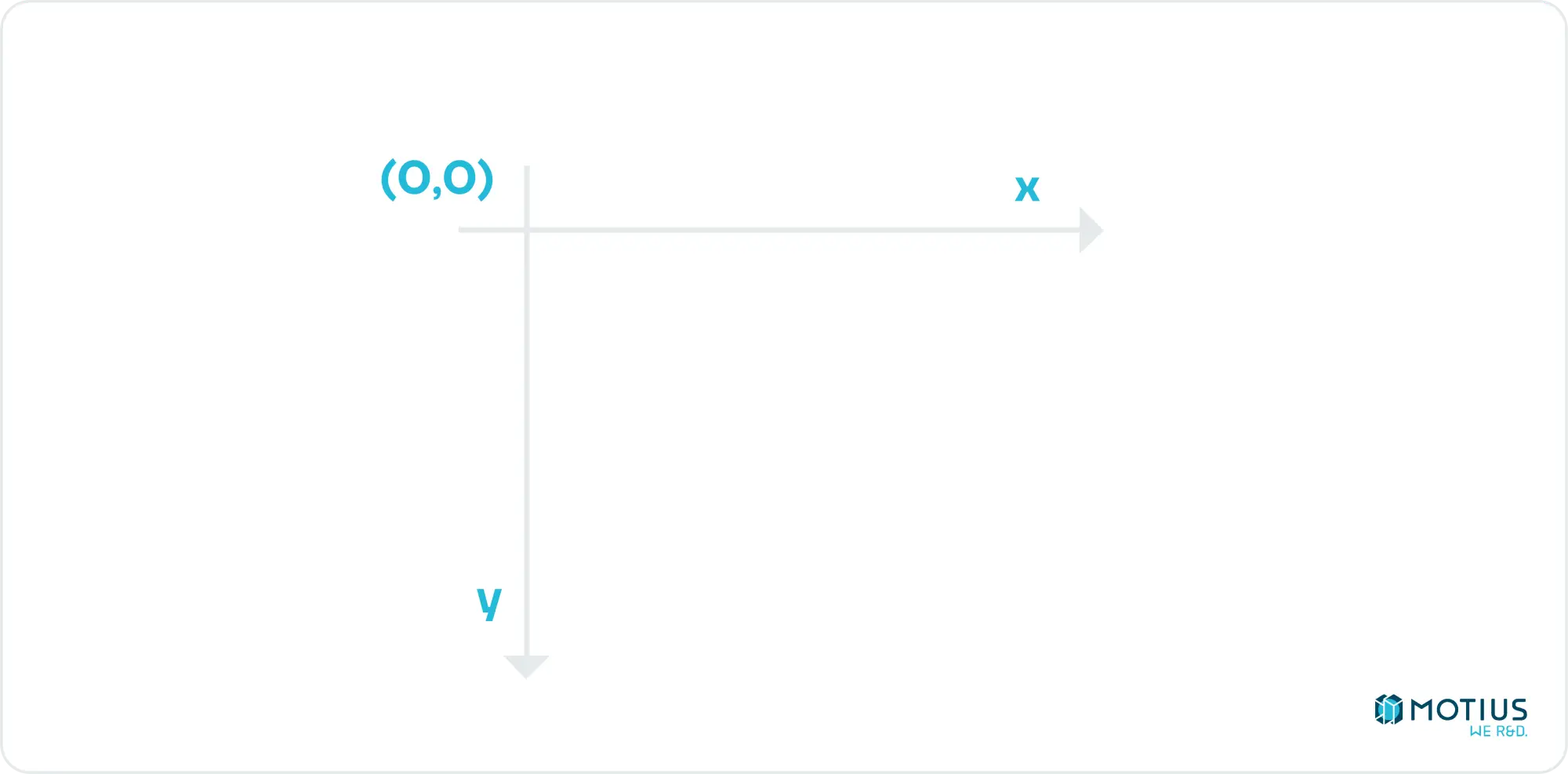
D.h. die obere linke Ecke ist der Ursprung. Unten ist die positive y-Richtung, und rechts ist die positive x-Richtung. Dies ist in der Computergrafik ziemlich üblich (da die obere linke Ecke [0, 0] sinnvoll ist, insbesondere wenn Sie Text schreiben, was ich vermute, ist das Alter, in dem diese Konvention begann).

Meine Implementierung folgt dem Beispiel meines Quelllehrbuchs und verwendet stattdessen:

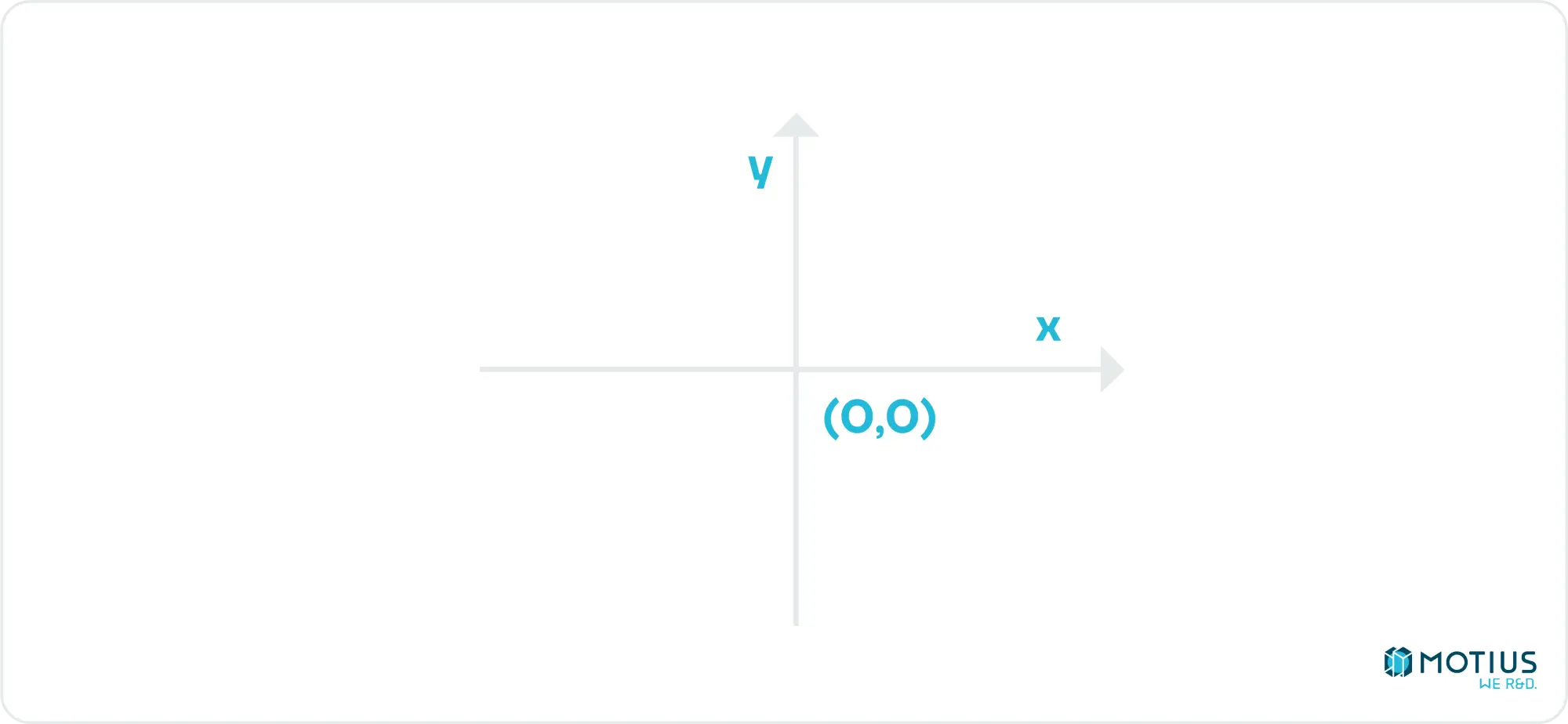
D.h. die Mitte der Leinwand ist der Ursprung. Rechts bleibt die positive x-Richtung, aber oben ist jetzt positiv y, wie Gott es beabsichtigt hat.

Von einer bis zu zwei Dimensionen: Linien zeichnen

Der Übergang vom Zeichnen einzelner Pixel zu horizontalen oder vertikalen Linien ist trivial, und wie jeder, der weiß, wie analoges Fernsehen funktioniert, weiß, wenn man horizontale Linien zeichnen kann, kann man alles zeichnen. Also können wir diesen Teil überspringen, oder?

Streng genommen, ja. Das Zeichnen von Linien ist jedoch eine sehr nützliche Sache in einem Renderer (Drahtgitter, beliebige Vektoren usw.) Wir werden es also schnell behandeln.

Diagonalen von 45 Grad sind nur geringfügig komplizierter als horizontale oder vertikale Linien. Zwischen diesen trivialen Fällen gibt es Bereiche, in denen wir für jedes x mehrere y-Werte einfärben müssen (oder umgekehrt). Es gibt einen Algorithmus namens "Bresenhams Linienalgorithmus", der dies sehr effizient mit nur ganzzahligen Operationen erledigt, was ihn für Computer sehr nützlich macht.

In dem spezifischen Oktanten der Steigung, die nach oben und rechts geht, die eher horizontal als vertikal sind:

Die Idee besteht darin, jeden x-Wert schrittweise zu durchlaufen und zu bestimmen, welcher y-Wert seinen Mittelpunkt am nächsten an der Ideallinie hat.

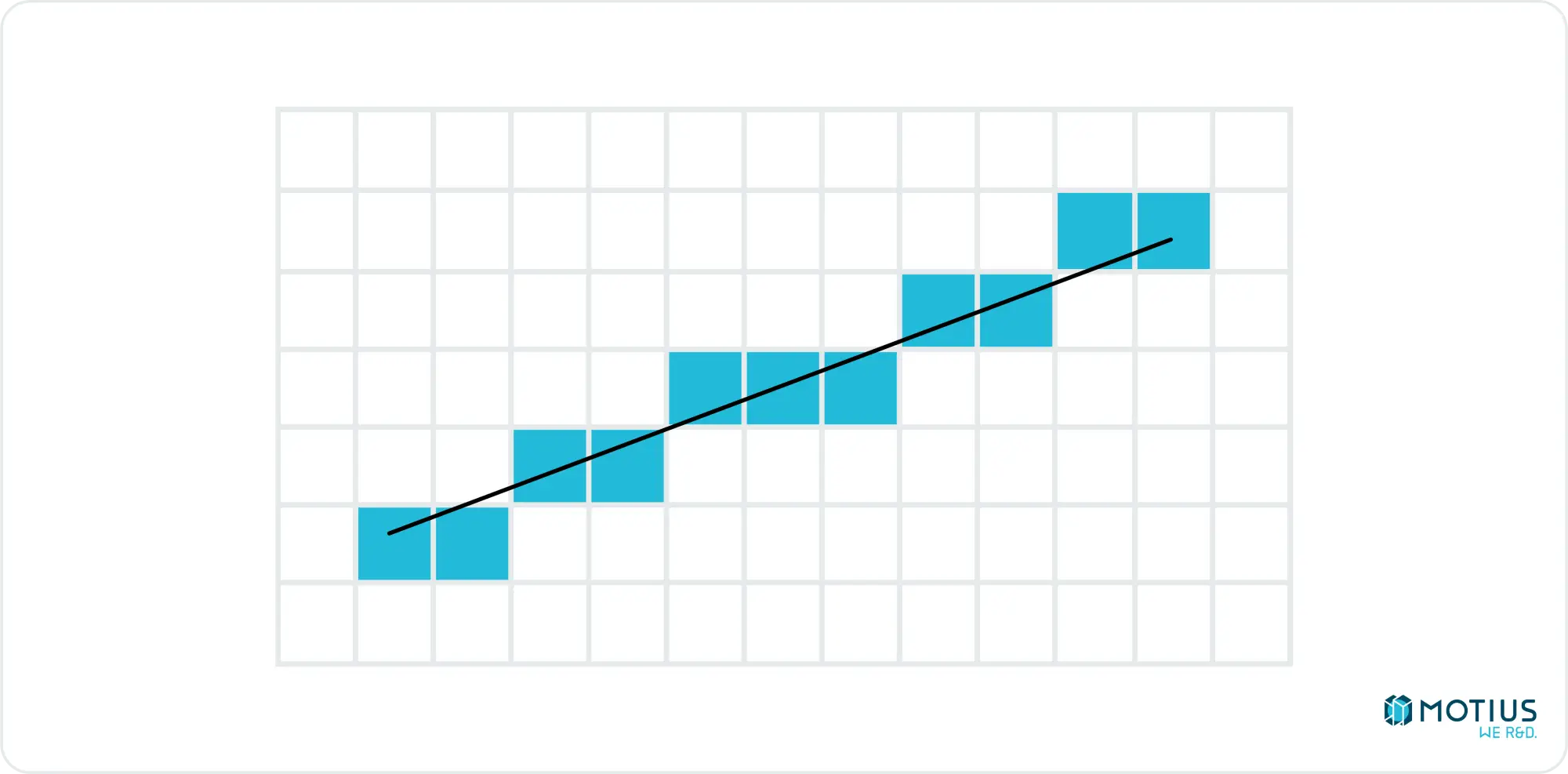
Dazu speichern wir im Wesentlichen, wie viel Aufwärtsbewegung bisher stattgefunden hat (manchmal auch als Fehlerakkumulation bezeichnet), und wenn genug vorhanden ist, erhöhen wir die aktive Zeile. Ich möchte nicht zu lange auf die Details eingehen, da es von Neugierigen leicht durchsucht und studiert werden kann, ich wollte es nur erwähnen, da es ein interessanter Algorithmus ist. Hier sehen Sie eine Javascript-Implementierung der Single-Quadrant-Lösung. Es kann leicht – wenn auch mühsam – auf die gesamte 2D-Ebene verallgemeinert werden.

 
function drawLine (context: CanvasRenderingContext2D, point0: Vector2, point1: Vector2, color: Color) {
  const dx = point1.x - point0.x
  const dy = point1.y - point0.y

  let D = (2 * dy) - dx
  let y = point0.y

  for (let x = point0.x; x <= point1.x; x++) {
    drawPixel(context, x, y, color)
    if (D > 0) {
      y += 1
      D = D + (2 * (dy - dx))
    } else {
      D = D + 2 * dy
    }
  }
}
 

Zeichnen von 2D-Dreiecken

Wie bereits erwähnt, kann jede 2D-Form mit horizontalen Linien gezeichnet werden. Die einzige Form, die uns für unseren 3D-Renderer wichtig ist, sind Dreiecke, daher schauen wir uns nun an, wie wir ein 2D-Dreieck in eine Reihe horizontaler Linien zerlegen.

Wenn du dir einen Bildschirm, der ein Dreieck rendert, sehr genau ansiehst, wirst du feststellen, dass es sich in Wirklichkeit nur um eine Reihe horizontaler Linien handelt. Du wirst auch deine Augen verletzen. Tu das nicht.

Um diese Reihe von Linien zu zeichnen, müssen wir zunächst den Anfangs- und Endpunkt jeder Linie finden. Für die y-Koordinate iterieren wir einfach vom obersten Punkt des Dreiecks zum untersten. Dann müssen wir alle x-Werte in einer bestimmten Zeile finden. Um dies zu tun, könnten wir wieder den Bresenham-Algorithmus verwenden. Ich werde hier jedoch einen einfacheren, allgemeineren linearen Interpolationsalgorithmus vorstellen:

 
function interpolate (i0: number, d0: number, i1: number, d1: number): number[] {
  if (i0 === i1) {
    return [ d0 ]
  }
  const values: number[] = []
  const a = (d1 - d0) / (i1 - i0)
  let d = d0
  for (let i = i0; i <= i1; i++) {
    values.push(d)
    d = d + a
  }
  return values
}
 

Wobei i0 und i1 unabhängige Variablen und immer ganze Zahlen sind, und d0 und d1 abhängige Variablen und Gleitkommazahlen sind. Die Fähigkeit, hier mit Gleitkommazahlen umzugehen, ist der Hauptvorteil gegenüber dem Bresenham-Algorithmus. Obwohl es für unsere ganzzahligen Pixelkoordinaten noch nicht unbedingt benötigt wird, werden wir später Gleitkommazahlen benötigen. Die Verwendung des gleichen Algorithmus für alles vereinfacht die Dinge.

Wenn du kein Cyborg bist oder einfach viel schlauer bist als ich, ist es wahrscheinlich nicht sofort offensichtlich, wie die Ausgabe dieser Funktion funktioniert, also nehmen wir ein einfaches Beispiel.

Interpolate(0, 0, 4, 3) gibt [0, 0.75, 1.5, 2.25, 3] aus. Aber was bedeutet das? Wir sagen, dass wir eine unabhängige Variable haben, die von 0 bis 4 reicht, und wir wollen die entsprechende abhängige Variable für jeden Wert der unabhängigen Variablen, wobei die erste 0 und die letzte 3 ist. Das ist alles eine umständliche Art, die lineare Interpolation zu sagen. Wenn unsere unabhängige Variable die y-Koordinate und x die abhängige Variable ist, dann haben wir gerade die x-Werte festgelegt, die wir benötigen, um eine Linie von [0, 0] bis [3, 4] zu zeichnen. (Wir müssten die Schwimmer natürlich abrunden).

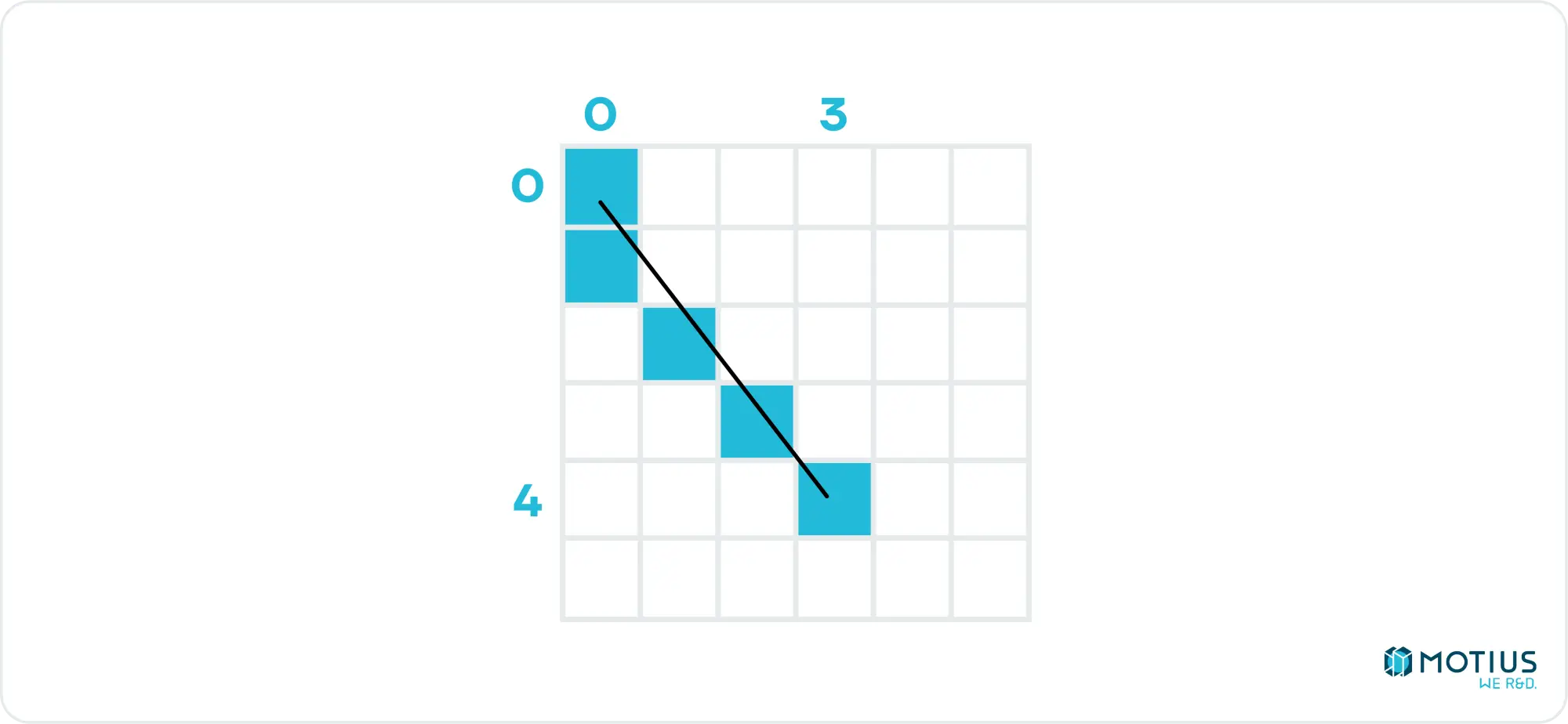
Zurück zu unserem Dreieck. Wenn wir die Eckpunkte v0, v1, v2 beschriften, wobei v0 die oberste und v2 die unterste ist, können wir sehen, dass entweder die linke oder die rechte Seite durch die Kante 02 und die andere durch die Zusammensetzung von 01 und 12 gegeben ist (es sei denn, v1 und v2 sind auf der gleichen Höhe, aber das kann glücklicherweise ignoriert werden, da es keine Linien zum gerenderten Dreieck beitragen würde).

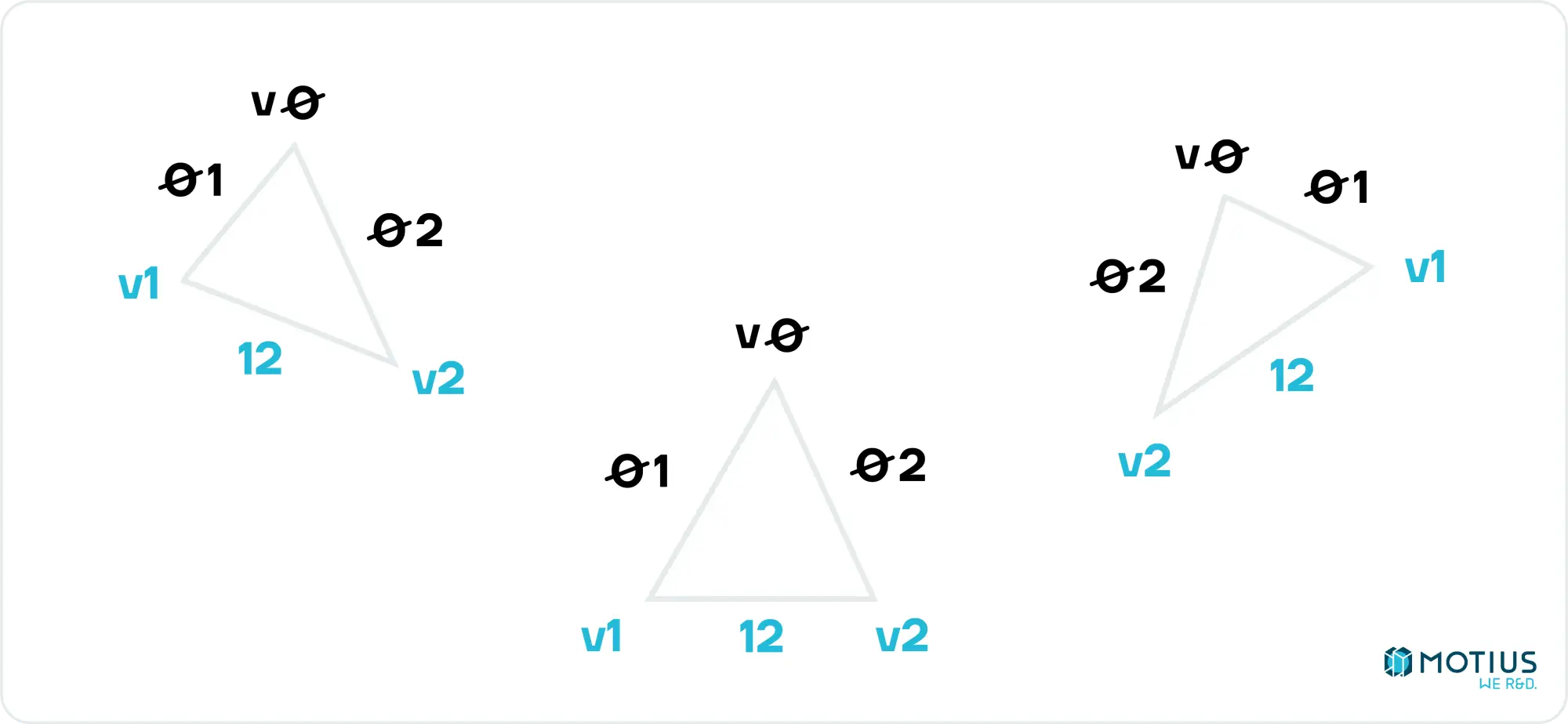
Wenn wir interpolieren(v0.y, v0.x, v1.y, v1.x) berechnen, erhalten wir eine Liste aller x-Werte in der Zeile 01 für jeden y-Wert. Ähnliches können wir für die anderen Kanten tun (und den doppelten Punkt von 01 & 12 rauswerfen, um zwei Listen mit x-Werten zu erhalten. Einer besteht aus allen Werten für die linken Seitenkanten und der andere aus der rechten Kante. Ein einfacher Vergleich verrät uns, was was ist. Das ist alles, was wir brauchen, um unser Dreieck zu zeichnen.

 
function drawFilledTriangle (context: CanvasRenderingContext2D, vertex0: Vector2, vertex1: Vector2, vertex2: Vector2, color: Color) {
  let [v0, v1, v2] = [
    vertex0,
    vertex1,
    vertex2,
  ].sort(sortByY)

  const x01 = interpolate(v0.y, v0.x, v1.y, v1.x)
  const x12 = interpolate(v1.y, v1.x, v2.y, v2.x)
  const x02 = interpolate(v0.y, v0.x, v2.y, v2.x)

  const x012 = [
    ...x01.slice(0, -1),
    ...x12,
  ]

  let xLeft, xRight: number[]

  const m = Math.floor(x012.length / 2)
  if (x02[m] < x012[m]) {
    xLeft = x02
    xRight = x012
  } else {
    xLeft = x012
    xRight = x02
  }

  for (let y = Math.floor(v0.y); y <= v2.y; y++) {
    const xL = Math.floor(xLeft[y - v0.y])
    const xR = Math.floor(xRight[y - v0.y])

    for (let x = xL; x <= xR; x++) {
      drawPixel(context, x, y, color)
    }
  }
}
 

Transformation koordinieren

Wir sind jetzt an dem Punkt, dass wir, wenn wir ein Dreieck in 2D definiert haben, es zeichnen können, aber wie kommen wir von einem 3D-Dreieck zu einem 2D-Dreieck? Um ein Dreieck in beiden Szenarien zu beschreiben, müssen wir nur die Koordinaten von drei separaten Punkten beschreiben. Die Frage ändert sich dann, wie wir einen 3D-Punkt in einen 2D-Punkt übersetzen, wenn eine Kameraposition und -drehung gegeben ist. Dann machen wir das einfach 3 Mal.

Beginnen wir einfach, mit der Kamera bei [0, 0] und in Richtung der positiven Z-Achse. Wir definieren unsere Rendering-Ebene in einiger Entfernung d von der Kamera, und sie hat eine bekannte Größe, sowohl in Bildschirmpixeln als auch in Weltkoordinaten.

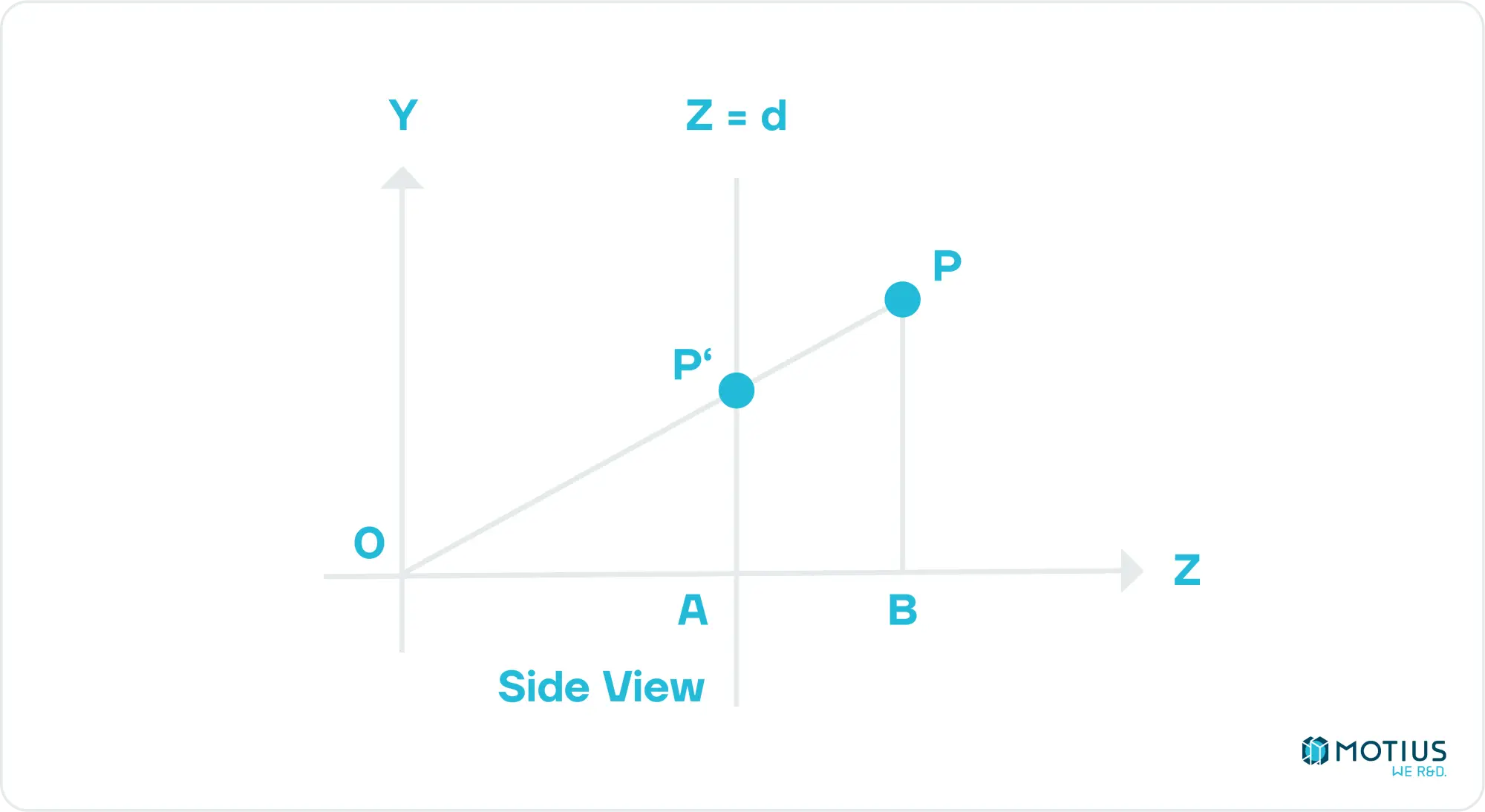
Zuerst wollen wir die Position unseres beliebigen Punktes finden, wenn er aus der Perspektive der Kamera auf unseren virtuellen Bildschirm projiziert wird. Wir können dies dann auf unseren Bildschirm skalieren. Aus dem obigen Bild geht hervor, dass die Z-Koordinate unseres projizierten Punktes offensichtlich gleich d ist. Um die anderen Koordinaten zu finden, können wir eine einfache Geometrie verwenden, um zu finden, dass _P'y = P_y.d / P_z ist. Wenn wir eine ähnliche Ansicht von oben nach unten konstruieren, sehen wir, dass _P'x = P_x.d / P_z ist.

Die Übersetzung aus dem 3D-Koordinatenraum in unseren Bildschirmkoordinatenraum ist ebenfalls recht einfach. Beides sind Rechtecke mit Größen, die wir definiert haben, so dass es nur eine Frage der Zuordnung von einer zur anderen ist. Wenn unser Ansichtsfenster in 3D-Koordinaten die Höhe und Breite V_h bzw. V_w und unsere Leinwand in 2D C_h und C_w hat, dann sollten die Koordinaten unseres Punktes auf unserem Bildschirm durch C_x = _P'x angegeben sein. C_w / V_w und C_y = P'y. C_h / V_h.

 
function viewportToCanvas (viewportCoordinates: Vector2): Vector2 {
  return {
    x: Math.round(viewportCoordinates.x * CANVAS_WIDTH / VIEWPORT_WIDTH),
    y: Math.round(viewportCoordinates.y * CANVAS_HEIGHT / VIEWPORT_HEIGHT),
  }
}

function projectVertex (vertex: Vector3): Vector2 {
  return viewportToCanvas({
    x: vertex.x * VIEWPORT_DISTANCE / vertex.z,
    y: vertex.y * VIEWPORT_DISTANCE / vertex.z,
  })
}

function draw3DTriangleToScreen (context: CanvasRenderingContext2D, vertex0: Vector3, vertex1: Vector3, vertex2: Vector3, color: Color) {
  const projectedVertecies = [
    projectVertex(vertex0),
    projectVertex(vertex1),
    projectVertex(vertex2),
  ]
  drawFilledTriangle(context, projectedVertices[0], projectedVertices[1], projectedVertices[2], color)
}
 

Betrete die Matrix: Die Benutzeroberfläche benutzerfreundlicher gestalten

Die obige Methode funktioniert und erreicht, was wir uns in dieser Folge vorgenommen haben. Aber für jede Szene, die komplexer ist als ein paar einzelne schwebende Dreiecke, wird es mühsam sein, sie tatsächlich zu verwenden, und ineffizient obendrein.

Nehmen wir das Beispiel eines Würfels, der sich im Raum bewegen und von einer Kamera beobachtet werden kann, die sich ebenfalls bewegen kann. Wir können die Transformationen jedes Mal durchführen, aber wir werden vieles wiederholen. Wenn wir uns einer linearen Algebra bedienen, können wir uns viel Mühe und Mühe ersparen.

Lasse uns zunächst unsere Daten ein wenig organisieren. Unsere Dreiecke gehören in der Regel zu einem Objekt. Und jeder der Eckpunkte innerhalb dieses Objekts wird Teil mehrerer Dreiecke sein. Wir können eine Struktur definieren, um diese Daten wie folgt zu speichern:

 
type Triangle = {
  vertices: [number, number, number]
  color: Color
}

type Mesh = {
  vertices: Vector3[]
  triangles: Triangle[]
}
 

Wobei der Dreieckstyp nur Indizes der Eckpunkte speichert, aus denen er besteht. Da wir gesagt haben, dass sich unsere Objekte bewegen können, müssen wir diese Bewegungsinformationen speichern. (Wir lassen es auch in verschiedenen Größen sein, wenn wir schon dabei sind).

 
type Transform = {
  rotation: RotationMatrix
  translation: Vector3
  scale: Vector3
}

type Object = {
  mesh: Mesh
  transform: Transform
}
 

Wobei die Rotationsmatrix gegeben ist durch:

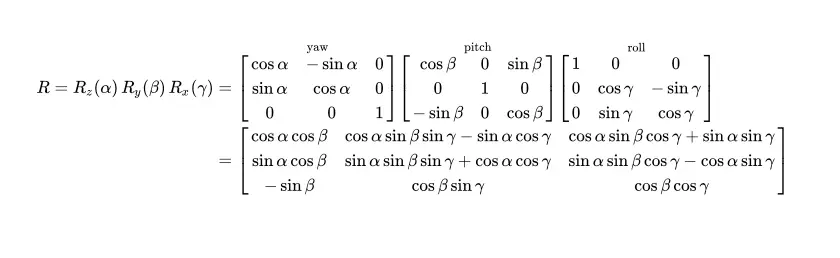
Eine Rotationsmatrix ist eine Möglichkeit, eine Drehung im Raum darzustellen. Und das ist ein Satz, der nicht viel aussagt. Die obigen Matrizen sind anfangs ziemlich schwer zu interpretieren, ich denke, es wird einfacher, wenn wir in 2D beginnen.

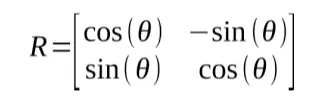
Multiplizieren wir dies mit einem 2D-Punkt entlang der x-Achse

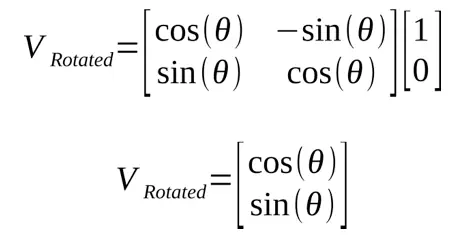
Dieses Ergebnis ist die Definition von Sinus und Kosinus in Bezug auf den Drehwinkel.

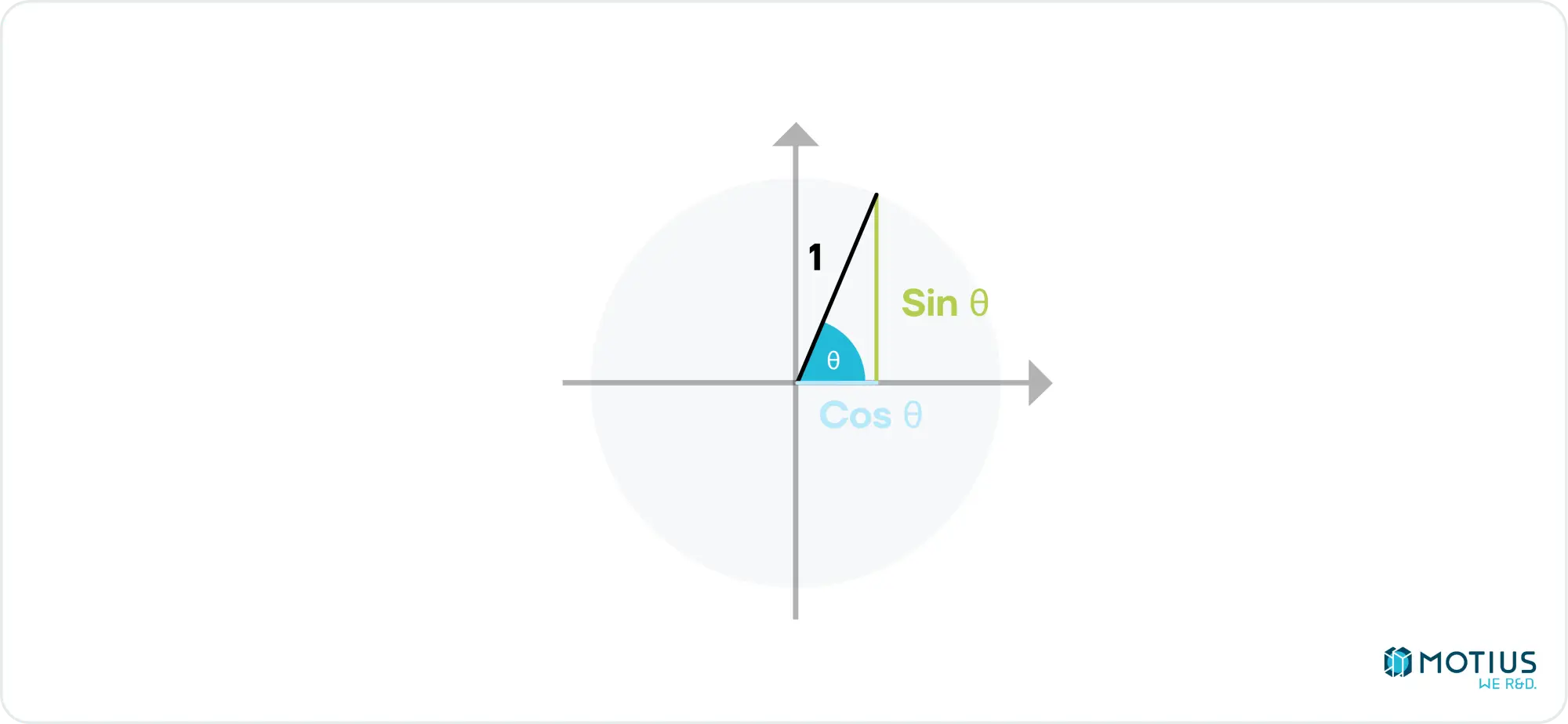
Wenn du die Augen zusammenkneifst (oder in Wikipedia nachsiehst), könntest du sehen, wie du von dem einfachen Beispiel hier zur vollständigen 3D-Rotationsmatrix mit 3 Achsen oben gelangen könntest. Ich habe hier nicht den Platz für eine detailliertere Ableitung, also wenn du immer noch verwirrt bist, schau in einem Lehrbuch für lineare Algebra nach. Zusätzlich zur Rotation müssen wir in der Lage sein, unser Objekt zu skalieren und zu verschieben. Skalentransformationen sind mit einer anderen Matrixmultiplikation ziemlich einfach durchzuführen:

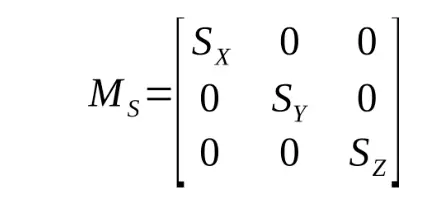
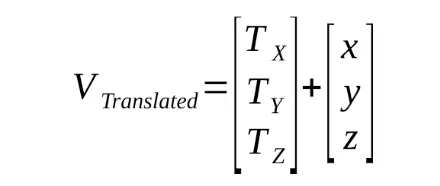
Übersetzungen lassen sich recht einfach durch einen Vektorzusatz darstellen:

Wenn wir jedoch einen Weg finden, dies mit einer dritten Multiplikation zu tun, können wir einen mächtigen Trick anwenden. Wir könnten eine einzelne Matrix für unser Modell erstellen:

_{M Modell} = M_T. M_R. _{M S}

Multipliziert mit dem Vektor, der die Position eines Scheitelpunkts relativ zu seinem übergeordneten Modell darstellt, ergibt sich die Position des Scheitelpunkts in Weltraumkoordinaten. Wir müssten diese Matrix nur einmal neu berechnen, wenn sich das Modell bewegt, und können sie wiederverwenden, während sie still steht, wodurch der Rechenaufwand pro gerendertem Frame erheblich reduziert wird.

Bevor wir diese multiplikative Translationsmatrix finden können, muss ich das Konzept der homogenen Koordinaten einführen. Betrachten Sie den Punkt (x, y, z). Wenn du nur einen Vector3 verwendest, um dies darzustellen, könntest du nicht sagen, ob es sich um einen Vektor oder eine bestimmte Position handelt. Wenn wir ein viertes Feld hinzufügen, das als eine Art Flagge fungiert, um anzuzeigen, dass es sich um einen Punkt handelt, hätten wir stattdessen (x, y, z, w). Wenn wir w = 0 als Vektor und jeden anderen Wert als Punkt behandeln, dann passieren einige interessante Dinge. Subtrahiert man zwei Punkte, erhält man den Vektor zwischen ihnen. Das Hinzufügen eines Vektors zu einem Punkt ergibt einen weiteren Punkt. Das macht alles Sinn. Es ist auch hier wichtig zu beachten, dass derselbe Punkt durch mehrere Werte von w dargestellt werden kann. Wenn Sie den homogenen Vektor durch den Skalar w dividieren, erhalten Sie w = 1, und dies wird als "kanonische" Darstellung des Vektors bezeichnet.

Jetzt, da wir dieses Konzept in der Tasche haben, siehst du schnell, dass Drehung und Skalierung gleich funktionieren, indem du einfach eine 4. Zeile und Spalte zu unseren Matrizen hinzufügst, mit einer 1 auf der Diagonalen und 0 an anderer Stelle (da das Drehen oder Skalieren eines Punktes zu einem Punkt führt, und das Gleiche gilt für Vektoren):

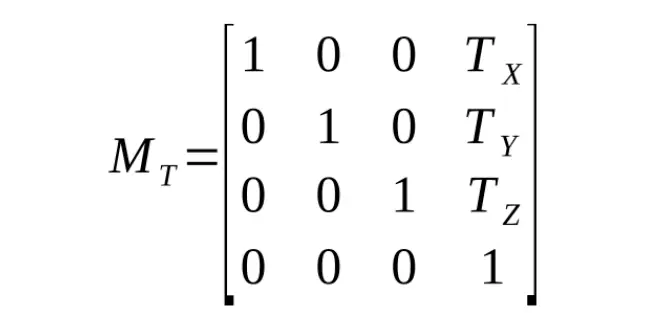
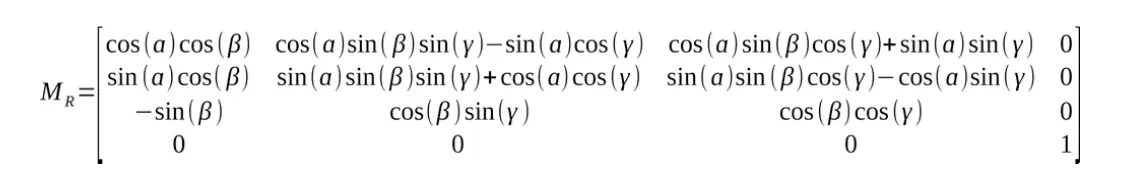
Aber wir haben immer noch keine Übersetzungsmatrix.

Wir benötigen es, um Folgendes zu tun:

Der Einfachheit halber wird dies auf den x-Wert reduziert:

Achse + Durch + Cz + D = x + T_x

Daher ist A = 1 und D = T_x. Ähnlich verhält es sich mit den anderen Koordinaten, und wir erhalten unsere Translationsmatrix:

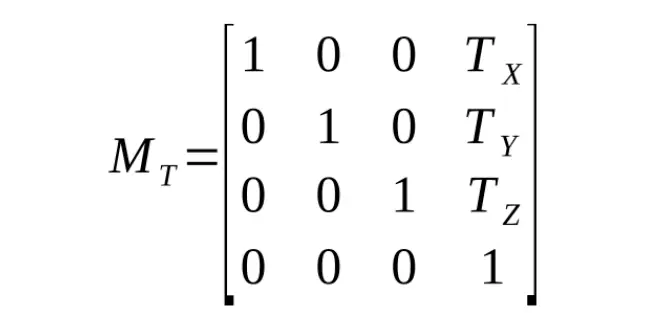
Objekte sind nicht das Einzige, was sich bewegen kann. Die Kamera kann das auch. Die Auswirkung, die dies auf die Position des Scheitelpunkts auf dem Bildschirm hat, ist identisch mit der Auswirkung, wenn das Objekt die inverse Transformation durchgeführt hätte. Auf ähnliche Weise und wenn wir alles rückwärts machen, erhalten wir:

_{M Kamera} = C ^R-1. C ^T-1

Dies muss nur einmal pro Bild aktualisiert werden, wenn sich die Kamera bewegt. Mit ihren kombinierten Kräften können wir nun die Position eines beliebigen Vertex relativ zur Kamera berechnen:

_{V Kamera} = M_Kamera. _M-Modell. _Modell V

Um die Bedienung der Kamera noch einfacher zu machen, können wir viele dieser Informationen tatsächlich reduzieren. Wenn wir keine holländischen Blickwinkel wollen, wird die Kamera nicht laufen. Auch das Skalieren der Kamera macht nicht wirklich viel Sinn, also lassen wir das fallen. (Ich vermute, wir haben dieses Konzept eigentlich nur expliziter mit der Leinwandgröße gehandhabt.)

 
type Camera = {
  position: Vector3,
  orientation: {
    pitch: number,
    yaw: number,
  }
}
 

Wenn wir uns also wieder nach oben arbeiten, können wir jetzt die Kameramatrix abrufen:

 
function createCameraMatrix(camera: Camera): HomogeneousMatrix {
  const inverseTranslation: HomogeneousMatrix = [
    [1, 0, 0, -camera.position.x],
    [0, 1, 0, -camera.position.y],
    [0, 0, 1, -camera.position.z],
    [0, 0, 0, 1],
  ]
  const inverseRotation = createInverseRotationMatrix(camera.orientation.pitch, camera.orientation.yaw)
  const homogeneousRotation: HomogeneousMatrix = [
    [...inverseRotation[0], 0],
    [...inverseRotation[1], 0],
    [...inverseRotation[2], 0],
    [0, 0, 0, 1],
  ]
  return multiplyMatrices(homogeneousRotation, inverseTranslation)
}

function createInverseRotationMatrix (pitch: number, yaw: number): RotationMatrix {
  const cosBeta = Math.cos(-yaw)
  const sinBeta = Math.sin(-yaw)

  const cosGamma = Math.cos(-pitch)
  const sinGamma = Math.sin(-pitch)

  return [
    [cosBeta, 0, sinBeta],
    [sinBeta * sinGamma, cosGamma, -cosBeta * sinGamma],
    [-sinBeta * cosGamma, sinGamma, cosBeta * cosGamma],
  ]
}

Mit dieser Kameramatrix können wir unsere Objekte nehmen und ihre Dreiecke in kamerarelative Koordinaten umwandeln:

 
function positionObject (object: Object, cameraMatrix: HomogeneousMatrix): PositionedTriangle[] {
  const matrix = multiplyMatrices(cameraMatrix, object.transformationMatrix)
  let transformedVertices: Vector3[] = object.model.vertices.map(vertex => {
    return applyTransform(vertex, matrix)
  })

  const triangles: PositionedTriangle[] = object.model.triangles.map(referenceTriangle => ({
    vertices: [
      transformedVertices[referenceTriangle.vertices[0]],
      transformedVertices[referenceTriangle.vertices[1]],
      transformedVertices[referenceTriangle.vertices[2]],
    ],
    color: referenceTriangle.color,
  }))

  return triangles

Wir können diese Dreiecke nun in unsere draw3DTriangleToScreen-Funktion einspeisen.

Wir haben jetzt also eine ziemlich benutzerfreundliche API, um jedes gut definierte Modell in unsere Szene zu zeichnen. Aber es gibt eine Menge verschwendetes Zeichnen, zum Beispiel das Zeichnen von Pixeln, die sich hinter anderen Pixeln befinden, und Dreiecke, die sich vollständig außerhalb des Bildschirms befinden. Wenn du diesen Code verwenden würdest, würdest du auch einige seltsame Artefakte entdecken, wenn sich das Objekt hinter der Kamera befindet. Alles besteht auch aus einzeln farbigen Dreiecken, was nur begrenzt anwendbar ist.

In der nächsten Folge gehe ich auf einige Optimierungen ein, die auch die Artefakte von Objekten hinter der Kamera auflösen. In einem anderen zukünftigen Beitrag werde ich darauf eingehen, wie man der Szene Beleuchtung hinzufügt.